A test of the leaf-ancestor metric for parse accuracy*

A test of the leaf-ancestor metric for parse accuracy*

Geoffrey Sampson and Anna Babarczy

School of Cognitive and Computing Sciences

University of Sussex

Falmer, Brighton BN1 9QH

England

Abstract

The GEIG metric for quantifying accuracy of parsing became influential through the Parseval programme, but many researchers have seen it as unsatisfactory. The leaf-ancestor (LA) metric, first developed in the 1980s, arguably comes closer to formalizing our intuitive concept of relative parse accuracy. We support this claim via an experiment which contrasts the performance of alternative metrics on the same body of automatically-parsed examples. The LA metric has the further virtue of providing straightforward indications of the location of parsing errors.

1 Introduction

One of us (Sampson 2000) has argued that what we call the “leaf-ancestor” (LA) metric is better than the Grammar Evaluation Interest Group (GEIG) metric used in the Parseval competition series (e.g. Black et al. 1991) as a way of quantifying the accuracy of automatic parses, in a context where gold-standard parses using a known scheme of node labelling are available. This paper presents an experiment comparing the performance of the two metrics on a sample of automatic-parser output.

The GEIG or Parseval metric, which counts the numbers of tagmas (multi-word grammatical units) correctly and incorrectly identified, from our point of view lays excessive weight on locating the exact boundaries of constructions.

As originally defined by Black et al. and as it is often applied, the GEIG metric takes no account of node labels at all: it only considers the location of brackets. And in consequence, this metric includes no concept of approximate correctness in identifying tagmas: a pair of brackets either enclose a sequence of words (or other terminal elements) exactly corresponding to a sequence bracketed off in the gold-standard parse, or not. The result is that “it is unclear as to how the score on [the GEIG] metric relates to success in parsing” (Bangalore, Sarkar, Doran, and Hockey 1998).

More recently (Magerman 1995, Collins 1997) a refined variant of the GEIG metric has been used which does check label identity as well as wordspan identity in matching tagmas between gold-standard and candidate parses. Nowadays, this variant of the GEIG metric is frequently used in preference to the original, label-free variant; but we shall argue that even this variant is inferior to the LA metric. We shall refer to the Black et al. (1991) and Collins (1997) variants of the GEIG metric as GEIG/unlabelled and GEIG/labelled respectively.

We think of “parsing” as determining what kind of larger elements are constituted by the small elements of a string that are open to direct observation. Identifying the exact boundaries of the larger elements is a part, but only one part, of that task. If, for instance, in the gold standard, words 5 to 14 are identified as a noun phrase, then a candidate parse which identifies a noun phrase as beginning at word 5 but ending at word 13, or word 15, should in our view be given substantial though not full credit; under the GEIG metric it is given no credit. The LA metric quantifies accuracy of parsing in this sense.

Incidentally, we believe that the LA metric was the earliest parse-assessment metric in the field, having been used, and briefly described in print, in the 1980s (Sampson, Haigh, and Atwell 1989: 278), though it was later eclipsed by the influential Parseval programme.

One strategy that has recently been adopted by a number of researchers who are dissatisfied with the Parseval approach to parse evaluation has been to use dependency rather than phrase-structure grammar formalisms. In principle, the LA metric can be applied equally well to dependency or to phrase-structure trees (Sampson 2000: 62–4). However, the advantages of LA assessment are clearer and more striking in connexion with phrase-structure trees, and in what follows we shall consider only this type of grammar formalism. Briscoe, Carroll, Graham, and Copestake (2002) propose a metric that counts the individual semantic relations encoded in a dependency structure, rather than what they call “more arbitrary details of tree topology”. That approach may be very suitable, for researchers who are committed to using grammar formalisms of the specific type required for it to be applicable. Our approach by contrast is to use a measure which applies equally well to a wide range of formalisms, but which assesses success and failure in a way that matches intuitive judgements of good or bad parsing better than the metric which has been standardly used until now.

2 The essence of leaf-ancestor assessment

The LA metric evaluates the parsing of an individual terminal element in terms of the similarity of the “lineages” of that element in candidate and gold-standard parse trees, where a lineage is essentially the sequence of node-labels for nodes on the unique path between the terminal element and the root node. The LA value for the parsing of an entire sentence or other many-word unit is simply the average of the values for the individual words. Apart from (we claim) yielding figures for parsing accuracy of complete sentences which succeed better than the GEIG metric in quantifying our intuitions about parse accuracy, the LA metric has the further practical virtue of identifying the location of parsing errors in a straightforward way.

We illustrate the general concept of LA assessment using one of the shortest sentences in our experimental data-set. (The nature of that data-set, and the gold-standard parsing scheme, will be discussed below.) The sentence runs two tax revision bills were passed. (Certain typographic details, including capitalization, inverted commas, and sentence-final punctuation marks, have been eliminated from the examples.) The gold-standard analysis, and the candidate analysis produced by an automatic parser, are respectively:

1G [S [N1 two [N1 tax revision ] bills ] were passed ]

1C [S [NP two tax revision bills ] were passed ]

(Here and below, “nG” and “nC” label gold-standard and candidate analyses for an example n.)

The automatic parser has failed to identify tax revision as a unit within the tagma headed by bills, and it has labelled that tagma NP rather than N1. Lineages for these tree structures are as follows, where for each terminal element the gold-standard lineage is shown to the left and the candidate lineage to the right of the colon, and within each of the paired lineages the Leaf end is to the Left and the Root end to the Right:

two N1 [ S : NP [ S

tax [ N1 N1 S : NP S

revision N1 ] N1 S : NP S

bills N1 ] S : NP ] S

were S : S

passed S ] : S ]

The only aspect of the relationship between this notation and the tree structures which is not self-explanatory is the inclusion of boundary markers (left and right square brackets) in many of the lineages. The reason for including these is that, without them, a set of lineages would not always uniquely determine a tree structure; for instance the structures “[P [Q a b ] [Q c ] ]” and “[P [Q a b c ] ]” would not be distinguishable, since the lineage for each terminal element in both cases would consist of the sequence Q P. A set of lineages uniquely determines the tree structure from which it is derived, if boundary markers are inserted by the following rules. (These rules, although intuitive enough once grasped, are unfortunately rather cumbersome to express in words.)

(i) A left-boundary marker is inserted in the lineage of a terminal element immediately before the label of the highest nonterminal beginning with that element, if there is such a nonterminal. Thus, in the gold-standard analysis for the example, two begins the entire sentence, so the left-boundary marker is placed in the lineage before S; tax begins the lower N1 tagma but is not initial in the higher N1 tagma which dominates it, so the left-boundary marker is placed before the lower N1 in the lineage; revision is not the first word of any tagma, so no left-boundary marker is included in its lineage.

(ii) Conversely, a right-boundary marker is inserted in the lineage of a terminal element immediately after the label of the highest nonterminal ending with that element, if there is such a nonterminal. Thus bills is the last word of the higher N1 tagma in the gold-standard analysis (but is not rightmost within the S tagma which dominates that N1), so a right-boundary marker is placed after N1 in the lineage; were is neither the first nor the last word of any tagma, so no boundary marker occurs in its lineage.

So, in the example above, the LA metric equates the accuracy with which the word two has been parsed with the degree of similarity between the two strings NP [ S and N1 [ S, it equates the parse-accuracy for tax with the degree of similarity between NP S and [ N1 N1 S, and so forth; for the last two words the lineages are identical, so the metric says that they have been parsed perfectly. We postpone discussion of our method for calculating string similarity until after we have discussed our experimental material.

3 The experimental material

Our experiment used a set of sentences from genre sections A and G of the SUSANNE Treebank (Sampson 1992) analysed by an automatic parser developed several years ago at the Universities of Cambridge and Sussex by Ted Briscoe and John Carroll (Carroll and Briscoe 1996); of those sentences for which the parser was able to produce a structure, a set of 500 was randomly chosen. For the purposes of illustrating the performance of the LA metric and comparing it with the GEIG metric, we wanted material parsed by a system that used a simple parsing scheme with a smallish vocabulary of nonterminal labels, and which made plenty of mistakes in applying the scheme to real-life data. There is no suggestion that the parses in our experimental data-set represent the present-day “state of the art” for automatic parsing; they certainly do not, but for current purposes that is a good thing. A state-of-the-art parser might make only small errors of a few kinds, and these might happen not to differentiate the performance of alternative parse-accuracy metrics very clearly. In order to discover which metric does best across the board at punishing bad mistakes heavily and small mistakes lightly, we need parser output containing a wide variety of errors of different degrees of gravity.

Likewise the use of SUSANNE as a source of experimental material may offer a better test than the obvious alternative, the Pennsylvania Wall Street Journal treebank, whose language samples are more homogeneous; Briscoe and Carroll (2002: 1500), quoting Srinivas (2000), suggest that that is so. We would not want to place much emphasis on this point: our test material was less diverse than the full SUSANNE treebank, and the small differences between the SUSANNE and WSJ figures in Srinivas’s table 7 (op. cit.: 134) might equally well be explained by the fact that his system was trained on WSJ material. But we agree with the general principle, expressed satirically by “Swift Redux” (2001 – not a pseudonym for either of ourselves), that it is unwise for the discipline to allow itself to depend too exclusively on research using material from a single newspaper.

The parsing scheme which the automatic parser was intended to apply used seven nonterminal labels, which we gloss with our own rather than Briscoe and Carroll’s labels:

S finite clause

VP nonfinite clause

NP noun phrase containing specifier

N1 noun phrase without specifier

PP prepositional phrase

AP adjectival or adverbial phrase

T “textual constituent”, defined by Briscoe and Carroll as a tagma enclosing “a sequence of sub-constituents whose relationship is syntactically indeterminate due to the presence of intervening, delimiting punctuation”

The use of these seven categories is defined in greater detail in documentation supplied to us, but for present purposes it is unnecessary to burden the reader with this material. The automatic-parser output occasionally included node-labels not on the above list (e.g. V, N2), but these were always regarded by the developers of the parser as mistakes.

Briscoe and Carroll’s original data included GEIG/unlabelled precision and recall scores for each automatic parse, assessed against the SUSANNE bracketing as gold standard. For the purposes of this experiment, the Evalb program (Sekine and Collins 1997) was used to produce GEIG/labelled precision and recall figures for the same data. In order to be able to compare our LA scores with single GEIG/labelled and GEIG/unlabelled scores for each sentence, we converted pairs of precision (P) and recall (R) figures to F-scores (van Rijsbergen 1979) by the formula , there being no reason to include a weighting factor to make precision accuracy count more than recall accuracy or vice versa.

One of us (Babarczy) constructed a set of gold-standard trees that could be compared with the trees output by the automatic parser, by manually adding labels from the seven-element Briscoe and Carroll label vocabulary to the SUSANNE bracketing, in conformity with the documentation on that seven-element vocabulary. Because the parsing scheme which the automatic parser was intended to apply was very different from the SUSANNE scheme, to a degree this was an artificial exercise. In some cases, none of the seven labels was genuinely suitable for a particular SUSANNE tagma; but one of them was assigned anyway, and such assignments were made as consistently as possible across the 500-sentence data-set. The admitted artificiality of this procedure did not seem unduly harmful, in the context of an investigation into the performance of a metric (as opposed to an investigation into the substantive problem of automatic parsing).

4 Calculation of lineage similarity

Leaf-ancestor assessment depends on quantifying the similarity between pairs of strings of node-labels. The standard metric for string similarity is Levenshtein distance (Levenshtein 1966), also called edit distance. The Levenshtein distance between two strings is the minimum cost for a set of insert, delete, and replace operations to transform one string into the other, where each individual operation has a cost of one. For instance, the Levenshtein distance between A B C B D and A D C B is two: the latter string can obtained from the former by replacing the second character with D and deleting the last character. If len(s) is the length of a string s, and Lv(s, t) is the Levenshtein distance between strings s and t, then a simple way of defining the similarity between candidate and gold-standard lineages c, g for a given terminal element would be to calculate it as 1 – Lv(c, g)/(len(c) + len(g)), which for any c, g must fall on the interval (0, 1). The accuracy of a candidate parse would be defined as the mean similarities of the lineage-pairs for the various words or other terminal elements of the string.

For our purposes this is a little too simple, because it does not allow for the fact that some labelling errors are more serious than others. For most schemes of natural-language parsing in practice, node labels will not be single letters but symbols with internal complexity; we want to be able to distinguish between cases where a label is entirely wrong, and cases where the candidate label is close to the gold-standard label although not identical to it. Furthermore, it has often been put to us that the seriousness of a mislabelling may sometimes be application-dependent (cf. Sampson 2000: 64–5). We allow for this by specifying that any particular application of LA assessment will involve defining a function from all possible pairs of node labels into the interval (0, 2); in assessing parse accuracy as above, simple Levenshtein distance is replaced by a modified calculation in which the cost of deletions and insertions remains one, but the cost of replacing one by another of a pair of node labels is determined by the function just described. The intuition here is that if two grammatical categories are entirely dissimilar, then for a parser to mistake one for the other amounts to two separate errors of failing to recognize the existence of a tagma of one kind, and falsely positing the existence of another type of tagma (a delete and an insert) – hence the cost should be two; but if the categories are more or less similar, then the lineages should be treated as less far apart. (Using this modification of Levenshtein distance, it remains true that the distance between two lineages must always fall on the interval (0, 1).)

In the case of Parseval-type competitions where the chief consideration is that rival systems should be judged on an equal footing, it may be appropriate to use the simplest version of LA assessment, in which replacement of any node label by any distinct label always costs two (labels are treated either as correct or as entirely wrong). But there is more to automatic parsing than competitions between rival systems. In a situation where parsing is applied to a practical task, it may be preferable to use a string-distance measure in which the costs of various label replacements are more differentiated.

The present experiment exemplifies this possibility by setting the cost of replacing a symbol by an unrelated symbol at 2, but the cost of a replacement where both symbols share the same first character at 0.5; thus partial credit is given for mistaking, say, a noun phrase for an N-bar, which is surely a lesser error than mistaking it for a subordinate clause. We are not suggesting that this particular cost function is likely to be ideal in practice, but it offers a clear, simple illustration of the possibility of partial credit for partly-correct labelling.

Applied to our short example sentence, the LA metric as defined above gives the scores for successive terminal elements shown in the left-hand column below:

0.917 two N1 [ S : NP [ S

0.583 tax [ N1 N1 S : NP S

0.583 revision N1 ] N1 S : NP S

0.917 bills N1 ] S : NP ] S

1.000 were S : S

1.000 passed S ] : S ]

To illustrate the calculation for the word revision: replacing either one of the N1 symbols by NP costs 0.5; deletion of the boundary symbol and the other N1 symbol each cost 1; 1 – (0.5 + 1 + 1)/(4 + 2) = 0.583.

The average for the whole sentence is 0.833. For comparison, the GEIG/unlabelled and GEIG/labelled F‑scores are 0.800 and 0.400.

5 Are the metrics equivalent?

The figure for the LA metric just quoted happens to be very similar to one of the two GEIG figures. An obvious initial question about the performance of the metrics over the data-set as a whole is whether, although the metrics are calculated differently, they perhaps turn out to impose much the same ranking on the candidate parses.

To this the answer is a clear no. Figures 1 and 2 compare the scores of the 500 parses on the LA metric with their scores on the GEIG/unlabelled and GEIG/labelled metrics respectively. In Figure 1, little or no correlation is visible between scores on the two metrics. (We find this surprising. If two alternative methods for measuring the same property yield uncorrelated results, one might have supposed that at least one of the methods could never be taken seriously at all.) Figure 2 does display a degree of clustering round a lower-left to upper-right axis, as expected, but the correlation is clearly quite weak.

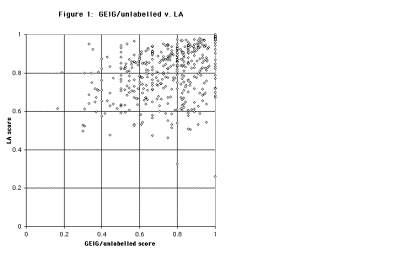
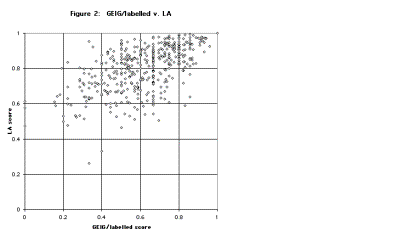
An extreme case of contrasting scores is (2), which corresponds to the most “north-westerly” point in Figures 1 and 2:

2G [S it is not [NP a mess [S you can make sense of ] ] ] G12:0520.27

2C [S it is not [NP a mess [S you can make sense ] ] of ] (0.333, 0.333, 0.952)

(Here and below, gold-standard analyses are followed by the SUSANNE location code of the first word – omitting the last three characters, this is the same as the Brown Corpus text and line number. The location for example (1) was A02:0790.51. Candidate parses are followed in brackets by their GEIG/unlabelled, GEIG/labelled, and LA scores, in that order.)

The LA and GEIG numerical scores for (2) are very different; but more important than the raw scores are the rankings assigned by the respective metrics, relative to the range of 500 examples. For both GEIG/labelled and GEIG/unlabelled, the parse of (2) is in the tenth (i.e. the lowest) decile; for LA, it is in the second decile. (The “nth decile”, for any of the metrics, refers to the set of examples occuping ranks 50(n – 1) + 1 to 50n, when the 500 candidate parses are ordered from best to worst in terms of score on that metric; for instance the second decile is the set of examples ranked 51 to 100. Where a group of examples share identical scores on a metric, for purposes of dividing the examples into deciles an arbitrary order was imposed on members of the group.)

The difference between the low GEIG scores and the high LA score for example (2) is a classic illustration of one of the standard objections to the GEIG metric. The parser has correctly discovered that the sentence consists of an S within NP within S structure, and almost every word has been given its proper place within that structure; just one word has been attached at the wrong level, but because this leads to the right-hand boundary of two of the three tagmas being slightly misplaced, the GEIG score is very low. We believe that most linguists’ intuitive assessment of example (2) would treat it as a largely-correct parse with one smallish mistake, not as one of the worst parses in the data-set – that is, the intuition would agree much better with the LA metric than with the GEIG metrics in this case.

An extreme case in the opposite direction (LA score lower than GEIG score) is (3), corresponding to the most “south-easterly” point in Figure 1:

3G [S yes , [S for they deal [PP with distress ] ] ] G12:1340.42

3C [T yes , [PP for they deal [PP with distress ] ] ] (1.0, 0.333, 0.262)

The GEIG/unlabelled metric gives 3C a perfect mark – all brackets are in the right place; but its LA score is very low, because two of the three tagmas are wrongly labelled. One might of course debate about whether, in terms of the Briscoe/Carroll labelling scheme, the root tagma should be labelled S rather than T, but that is not to the point here. The relevant point is that, if the target is the gold-standard parse shown, then a metric which gives a poor score to 3C is performing better than a metric which gives it a perfect score.

For example (3), GEIG/labelled performs much better than GEIG/unlabelled. Where parsing errors relate wholly or mainly to labelling rather than to structure, that will be so. But we have seen in the case of (2), and shall see again, that there are other kinds of parsing error where GEIG/labelled is no more, or little more, satisfactory than GEIG/unlabelled.

6 Performance systematically compared

In order systematically to contrast the performance of the metrics, we need to focus on examples for which the ranking of the candidate parse is very different under the different metrics, which implies checking cases whose parses are among the lowest-ranked by one of the metrics. It would be little use to check the highest-ranked parses by either metric. Many candidates are given perfect marks by the LA metric, because they are completely accurate, in which case they will also receive perfect GEIG marks. (In both Figures 1 and 2, the data point at (1.0, 1.0) represents 63 of the 500 examples.) Some candidates receive perfect GEIG/unlabelled marks but lower LA (and GEIG/labelled) marks, however this merely reflects the fact that GEIG/unlabelled ignores labelling errors.

We have checked how many examples from the lowest GEIG/unlabelled and GEIG/labelled deciles fall into the various LA deciles, and how many examples from the lowest LA decile fall into the various GEIG/unlabelled and GEIG/labelled deciles. These are the results:

LA deciles for GEIG/unlabelled 10th decile:

1st 0

2nd 1

3rd 3

4th 2

5th 2

6th 4

7th 8

8th 7

9th 11

10th 12

LA deciles for GEIG/labelled 10th decile:

1st 0

2nd 1

3rd 1

4th 0

5th 0

6th 1

7th 7

8th 8

9th 13

10th 19

GEIG/unlabelled deciles for LA 10th decile:

1st 1

2nd 0

3rd 4

4th 9

5th 3

6th 8

7th 4

8th 5

9th 4

10th 12

GEIG/labelled deciles for LA 10th decile:

1st 0

2nd 0

3rd 1

4th 1

5th 3

6th 8

7th 5

8th 5

9th 8

10th 19

The examples of particular interest are those counted in the higher rows of these four tables, which are assessed very differently by the alternative metrics.

The GEIG/unlabelled and GEIG/labelled 10th-decile, LA 2nd-decile example is (2), already discussed above. The GEIG/labelled 10th-decile, LA 3rd-decile example (and this is also one of the GEIG/unlabelled 10th-decile, LA 3rd-decile examples) is (4):

4G [S then he began [VP to speak [PP about [NP the tension [PP in art ] [PP between [NP the mess [N1 and form ] ] ] ] ] ] ] G12:0610.27

4C [S then he began [VP to speak [PP about [NP the tension ] ] [PP in [N1 art [PP between [NP the mess ] ] [N1 and form ] ] ] ] ] (0.353, 0.353, 0.921)

The two further GEIG/unlabelled 10th-decile, LA 3rd-decile cases are:

5G [S Alusik then moved Cooke across [PP with [NP a line drive [PP to left ] ] ] ] A13:0150.30

5C [S Alusik then moved Cooke across [PP with [NP a line drive ] ] [PP to left ] ] (0.500, 0.500, 0.942)

6G [S [NP their heads ] were [PP in [NP the air ] ] sniffing ] G04:0030.18

6C [S [NP their heads ] were [PP in [NP the air sniffing ] ] ] (0.500, 0.500, 0.932)

Examples (5) and (6) are essentially similar to (2) above, since all three concern errors about the level at which a sentence-final element should be attached. The LA scores are marginally lower than for (2), because the misattached elements comprise a higher proportion of total words in the respective examples. In (5) a two-word phrase rather than a single word is misattached, and in (6) the misattached element is a single word but the sentence as a whole is only seven words long while example (2) contains ten words. Intuitively it is surely appropriate for a misattachment error involving a higher proportion of total words to be given a lower mark, but for these candidates nevertheless to be treated as largely correct. (Notice that the candidate parse for (5) verges on being a plausible alternative interpretation of the sentence, i.e. not mistaken at all. It is only the absence of the before left which, to a human analyst, makes it rather certain that our gold-standard parse is the structure corresponding to the writer’s intended meaning.)

The candidate parse for (4) contains a greater variety of errors, and we would not claim that in this case it is so intuitively clear that the candidate should be ranked among the above-average parses. Notice, though, that although several words and tagmas have been misattached, nothing has been identified as a quite different kind of tagma from what it really is (as for they deal with distress in (3) above was identified as a prepositional phrase rather than subordinate clause). Therefore our intuitions do not clearly suggest that the candidate should be ranked as worse than average, either; our intuitions are rather indecisive in this case. In other cases, where we have clear intuitions, the LA ranking agrees with them much better than the GEIG ranking.

Turning to cases where LA gives a much lower ranking than GEIG: the most extreme case is (3), already discussed. The LA 10th-decile, GEIG/labelled 3rd decile case (which is also one of the GEIG/unlabelled 3rd-decile cases) is (7):

7G [S [NP its ribs ] showed , [S it was [NP a yellow nondescript color ] ] , [S it suffered [PP from [NP a variety [PP of sores ] ] ] ] , [S hair had scabbed [PP off [NP its body ] ] [PP in patches ] ] ] G04:1030.15

7C [T [S [NP its ribs ] showed ] , [S it was [NP a yellow nondescript color ] ] , [S it suffered [PP from [NP a variety [PP of sores ] ] ] ] , [S hair had scabbed off [NP its body ] [PP in patches ] ] ] (0.917, 0.833, 0.589)

There are large conflicts between candidate and gold-structure parses here: the candidate treats the successive clauses as sisters below a T node, whereas under the SUSANNE analytic scheme the gold-standard treats the second and subsequent clauses as subordinate to the first, with no T node above it; and the candidate fails to recognize off as introducing a PP. The presence v. absence of the T node, because it occurs at the very top of the tree, affects the lineages of all words and hence has a particularly large impact on LA score. (Sampson 2000: 66 discussed the fact that the LA metric penalizes mistakes more heavily if they occur higher in a tree, because mistakes high in a tree affect the lineages of many words. This might be seen as an undesirable bias; on the other hand, one commentator has suggested to us that this feature of the LA metric is a positive virtue, because parse errors higher in trees tend to have more severe practical consequences for NLP applications.)

The three other LA 10th-decile, GEIG/unlabelled 3rd-decile cases are:

8G [S [S when [NP the crowd ] was asked [S whether it wanted [VP to wait [NP one more term ] [VP to make [NP the race ] ] ] ] ] , it voted no – [S and there were [NP no dissents ] ] ] A01:0980.06

8C [T [S [PP when [NP the crowd ] was asked [PP whether it wanted [VP to wait [NP one more term ] [VP to make [NP the race ] ] ] ] ] , it voted no ] – [S and there were [NP no dissents ] ] ] (0.952, 0.667, 0.543)

9G [S [S we wo +n't know [NP the full amount ] [S until we get [NP a full report ] ] ] , Wagner said ] A09:0520.12

9C [T [S we wo +n’t know [NP the full amount ] [PP until we get [NP a full report ] ] ] , [S Wagner said ] ] (0.909, 0.545, 0.531)

10G [S [S [NP her husband ] was lying [PP on [NP the kitchen floor ] ] ] , police said ] A19:1270.48

10C [T [S [NP her husband ] was lying [PP on [NP the kitchen floor ] ] ] , [S police said ] ] (0.909, 0.727, 0.627)

Each of these involves the same problems as (7) of presence v. absence of a root T node and co-ordinate v. subordinate relationships between successive clauses. Example (8) includes further large discrepancies: when and whether are both treated as initiating prepositional phrases rather than clauses, though neither word has a prepositional use (in terms of the traditional part-of-speech classification as represented in published dictionaries – this may be another case where the candidate parse is correct in terms of special assumptions about linguistic theory incorporated in the software which produced it, but the relevant point for us is that if 8G is the gold standard then 8C is badly wrong). Example (9) has a similar error involving until (this is more understandable, since until can be a preposition). Intuitively, to the present authors, the LA metric seems correct in characterizing (8) and (9) as two of the cases where the candidate parse deviates furthest from the gold standard, rather than as two of the best parses. The case of (10) is admittedly less clearcut.

Some readers may find this section unduly concerned with analysts’ intuitions as opposed to objective facts. But, if the question is which of two metrics better quantifies parsing success, the only basis for comparison is people’s intuitive concept of what ought to count as good or bad parsing. Both metrics give perfect scores to perfect matches between candidate and gold-standard structure; which departures from perfect matching ought to be penalized heavily can only be decided in terms of “educated intuition”, that is intuition supported by knowledge and discussion of the issues. It would not be appropriate to lend such intuitions the appearance of objectivity and theory-independence by “counting votes” from a large number of subjects. (Since the GEIG metric is widely known, raw numbers from an exercise like that could have as much to do with the extent to which individual informants were aware of that metric as with pre-theoretical responses to parse errors.) Deciding such an issue in terms of averaged subject responses would be as inappropriate as choosing between alternative scientific theories by democratic voting. Rather, the discussion should proceed as we have conducted it here, by appealing to readers’ and writers’ individual intuitions with discussion of particular examples.

7 Local error information

Different accuracy rankings assigned to complete parses are not the only reason for preferring the LA to the GEIG metric. Another important difference is the ability of the LA metric to give detailed information about the location and nature of parse errors.

Consider, for instance, example (11), whose gold-standard and candidate analyses are:

11G [S however , [NP the jury ] said [S it believes [S [NP these two offices ] should be combined [VP to achieve [N1 greater efficiency ] [VP and reduce [NP the cost [PP of administration ] ] ] ] ] ] ] A01:0210.15

11C [S however , [NP the jury ] said [S it believes [NP these two ] [S offices should be combined [VP to [VP achieve [N1 greater efficiency ] [VP and reduce [NP the cost [PP of administration ] ] ] ] ] ] ] ] (0.762, 0.667, 0.889)

The score of 0.889 assigned by the LA metric to this candidate analysis, like any LA score, is the mean of scores for the individual words. For this example, those are as follows:

1.000 however [ S : [ S

1.000 , S : S

1.000 the [ NP S : [ NP S

1.000 jury NP ] S : NP ] S

1.000 said S : S

1.000 it [ S S : [ S S

1.000 believes S S : S S

0.667 these NP [ S S S : [ NP S S

0.750 two NP S S S : NP ] S S

0.667 offices NP ] S S S : [ S S S

1.000 should S S S : S S S

1.000 be S S S : S S S

1.000 combined S S S : S S S

1.000 to [ VP S S S : [ VP S S S

0.800 achieve VP S S S : [ VP VP S S S

0.923 greater [ N1 VP S S S : [ N1 VP VP S S S

0.923 efficiency N1 ] VP S S S : N1 ] VP VP S S S

0.769 and [ S VP S S S : [ VP VP VP S S S

0.727 reduce S VP S S S : VP VP VP S S S

0.800 the [ NP S VP S S S : [ NP VP VP VP S S S

0.769 cost NP S VP S S S : NP VP VP VP S S S

0.824 of [ PP NP S VP S S S : [ PP NP VP VP VP S S S

0.824 administration PP NP S VP S S S ] : PP NP VP VP VP S S S ]

The display shows that, according to the LA metric, the early part of the sentence is parsed perfectly, and that the worst-parsed part is these two offices. That seems exactly right; in the correct analysis, these three words are a NP, subject of the clause which forms the object of believe, but the automatic parser has interpreted believe as a ditransitive verb with these two as indirect object, and has treated offices as grammatically unrelated to these two. Intuitively, these are gross mistakes. The next stretch of erroneous parsing is from achieve to the end, where each word’s mark is pulled down by the error of taking achieve to open a subordinate VP within the VP initiated by the preceding to. Relative to the SUSANNE scheme used here as gold standard, this also seems a bad error. It is an understandable consequence of the fact that the Briscoe/Carroll automatic parser was based on a parsing scheme that made different theoretical assumptions about grammar, but in the present target scheme no English construction ought to be analysed as “[VP to [VP ...”.

We would not pretend that our intuitions are so refined that they positively justify a score for reduce which is marginally lower than those for the surrounding words, or positively justify the small difference between 0.727 as the lowest score in the second bad stretch and 0.667 in the earlier stretch; the present authors’ intuitions are vaguer than that. But notice that, as it stands, the GEIG metric offers no comparable technique for identifying the locations of bad parsing performance within parsed units; it deals in global scores, not local scores. True, one can envisage ways in which the GEIG metric might be developed to yield similar data; it remains to be seen how well that would work. (Likewise, the GEIG/labelled metric could be further developed to incorporate the LA concept of partial matching between label pairs. On the other hand, there is no way that GEIG could be adapted to avoid the unsatisfactory performance exemplified by (2) above.)

Using the LA metric, researchers developing an automatic parser in a situation where large quantities of gold-standard analyses are available for testing should easily be able to identify configurations (e.g. particular grammatical words, or particular structures) which are regularly associated with low scores, in order to focus parser development on areas where further work is most needed. If the parsing scheme used a larger variety of nonterminal labels, one would expect that individual nonterminals might regularly be associated with low scores, though with the very austere nonterminal vocabulary of the Briscoe/Carroll scheme that is perhaps less likely to be so. Even with a small-vocabulary scheme like this, though, one might expect to find generalizations such as “when a subordinate S begins with a multi-word NP, the parser tends to fail”. Note that we are not saying that this is a true generalization about the particular automatic parser used to generate the data under discussion; one such mistake occurs in the example above, but we do not know whether this is a frequent error or a one-off. Any automatic parser is likely to make errors in some recurring patterns, though; the LA metric is potentially an efficient tool for identifying these, whatever they happen to be.

8 Conclusion

From these results, we would argue that the leaf-ancestor metric comes much closer than the GEIG metric to operationalizing our intuitive concepts of accurate and inaccurate parsing.

Someone looking for reasons to reject the LA metric might complain, correctly, that the algorithm for calculating it is much more computation-intensive than that for the GEIG metric. But intensive computation is not a problem in modern circumstances.

More important: there is no virtue in a metric that is easy to calculate, if it measures the wrong thing.

*The research reported here was supported in part by the Economic and Social Research Council (UK) under grant R000 23 8746. We are very grateful to John Carroll for supplying us with the experimental material, generating the GEIG/labelled data, and discussing the material with us; and we are grateful for further discussion by participants at the workshop “Beyond PARSEVAL: Towards Improved Evaluation Measures for Parsing Systems”, Las Palmas, Canary Islands, 2 June 2002 (where a version of the paper was presented), and to anonymous referees for this journal.

References

Bangalore, S., Sarkar, A., Doran, Ch., and Hockey, B.A.. (1998) “Grammar and parser evaluation in the XTAG project”. In J.A. Carroll, ed., Proceedings of Workshop on the Evaluation of Parsing Systems, 1st International Conference on Language Resources and Evaluation, Granada, Spain, 26 May 1998 (Cognitive Science Research Papers 489, University of Sussex).

Black, E., Abney, S., Flickinger, D., Gdaniec, C., Grishman, R., Harrison, P., Hindle, D., Ingria, R., Jelinek, F., Klavans, J., Liberman, M., Marcus, M., Roukos, S., Santorini, B., and Strzalkowski, T. (1991) “A procedure for quantitatively comparing the syntactic coverage of English grammars”. In Proceedings of the Speech and Natural Language Workshop, Defence Advanced Research Projects Agency (DARPA), February 1991, Pacific Grove, Calif., pp. 306–11. Morgan Kaufmann.

Briscoe, E.J., and Carroll, J.A. (2002) “Robust accurate statistical annotation of general text”. In Proceedings of the 3rd International Conference on Language Resources and Evaluation, Las Palmas, Canary Islands, vol. v, pp. 1499–1504.

Briscoe, E.J., Carroll, J.A., Graham, J., and Copestake, A. (2002) “Relational evaluation schemes”. In Proceedings of the Workshop “Beyond Parseval – towards improved evaluation measures for parsing systems”, 3rd International Conference on Language Resources and Evaluation, Las Palmas, Canary Islands, 4–8.

Carroll, J.A., and Briscoe, E.J. (1996) “Apportioning development effort in a probabilistic LR parsing system through evaluation”. In Proceedings of the ACL/SIGDAT Conference on Empirical Methods in Natural Language Processing, University of Pennsylvania, 92–100.

Collins, M. (1997) “Three generative, lexicalised models for statistical parsing”. In Proceedings of the 35th Annual Meeting of the Association for Computational Linguistics and 8th Conference of the European Chapter of the Association for Computational Linguistics, 7–12 July 1997, Madrid. Morgan Kaufmann.

Levenshtein, V.I. (1966) “Binary codes capable of correcting deletions, insertions, and reversals”, Soviet Physics – Doklady 10.707–10 (translation of Russian original published in 1965).

Magerman, D.M. (1995) “Statistical decision-tree models for parsing”. In Proceedings of the 33rd Annual Meeting of the Association for Computational Linguistics, 26-30 June 1995, Cambridge, Mass., pp. 276-83. Morgan Kaufmann.

van Rijsbergen, C.J. (1979) Information Retrieval, 2nd edn. Butterworths (London).

Sampson, G.R. (1992) The SUSANNE Treebank. Up-to-date release available from www.grsampson.net → “downloadable research resources”.

Sampson, G.R. (2000) “A proposal for improving the measurement of parse accuracy”. International Journal of Corpus Linguistics 5.53-68.

Sampson, G.R., Haigh, R., and Atwell, E.S. (1989) “Natural language analysis by stochastic optimization”, Journal of Experimental and Theoretical Artificial Intelligence 1.271–87.

Sekine, S. and Collins, M. (1997) Evalb software at www.cs.nyu.edu/cs/projects/proteus/evalb/.

Srinivas, B. (2000) “A lightweight dependency analyzer for partial parsing”. Natural Language Engineering 6.113–38.

“Swift Redux” (2001) “A modest proposal”. ELSNews 10.2, Summer 2001, p. 7.