Depth in English grammar
Geoffrey Sampson
University of Sussex
ABSTRACT
Corpus data are used to investigate Yngve’s claim
that English usage avoids grammatical structures in which the number of left
branches between any word and the root node of a sentence exceeds some fixed
limit. The data do display a
marked bias against left-branching, but the pattern of word-depths does not
conform to Yngve’s concept of a sharp limit. The bias could alternatively reflect a statistical
invariance in the incidence of left-branching, but whether this is so depends
on how left-branching is counted.
Six nonequivalent measures are proposed; it turns out that one (and only
one) of these yields strikingly constant figures for left-branching in
real-life sentences over a wide range of lengths. This is not the measure suggested by Yngve’s formulation; it
is the measure whose invariance is arguably the most favourable for
computational tractability.
1. History and implications of the Yngve Hypothesis
Victor Yngve drew attention (1960, 1961) to an
asymmetry in English grammar favouring right-branching over left-branching
structures: although various
individual grammatical constructions create left-branching, Yngve believed that
the use of these constructions is in practice constrained in such a way that
the ‘depth’ of any word in a sentence never exceeds some fixed limit, perhaps
seven. He offered an explanation
for this in terms of psychological processing mechanisms. Lees (1961) and Fodor et al. (1974:
408ff.) argued that the relevant psychological considerations are more complex
than Yngve supposed, and that the depth constraints in languages such as
Japanese and Turkish are quite different from that in English.
Note
that the term ‘depth’, in Yngve’s usage, refers purely to the quantity of
left-branching contained in the path linking a terminal node to the root node
of a grammatical tree structure (we shall become more precise shortly about how
this is counted). It is necessary
to stress this to avoid misunderstanding, because the term ‘depth’ is used
quite differently in connexion with tree structures by computer scientists, for
whom the depth of a terminal node is the total number of branches (of any kind)
between itself and the root. Thus,
for a computer scientist, the rightmost terminal node of a tree may have a
large depth, but for Yngve the depth of the last word of a sentence is
necessarily zero. Yngve’s papers
on this topic have attained such classic status in linguistics that I have
chosen to follow his usage here.
The computer scientists’ ‘depth’ is a quantity which plays no part in
the present discussion, so I have not needed to adopt any particular term for
it.[1]
The
question of left-branching became linked for linguists with that of multiple
central embedding (Miller & Chomsky 1963, Reich 1969), which is claimed to
be constrained very tightly indeed.
Occasionally it is suggested (e.g. Lyons 1991: 116) that Yngve’s
hypothesis might have resulted from taking what is in reality a constraint on
central embedding to be a more general constraint on left-branching. But these issues should be kept
distinct. There unquestionably is
a strikingly low incidence in English of left-branching in general ‹ that is,
of multi-word constituents occurring anywhere other than as rightmost daughters
of their containing constructions.
One of the most immediately noticeable features of any
grammatically-analysed English corpus which uses brackets to delimit
constituents is the frequent occurrence of long sequences of right brackets at
the same point in a text, while sequences of adjacent left brackets are few and
short. On the other hand the
empirical facts about central embedding are less clear. De Roeck et al. (1982) and Sampson
(1996) give evidence that the kinds of construction claimed by writers such as
Church (1982: 24 n. 32) and Stabler (1994: 315-316) to be ‘unacceptable’ do
quite often occur in ordinary usage in English and other languages. There may be a special avoidance of
central embedding; alternatively, the alleged rarity of multiple central
embedding might just reflect the familiar principle that, when one counts
examples of anything, the more detailed the criterion which examples are
required to meet the fewer cases one will find. This paper will study the general English tendency for
multi-word constituents to occur at the end of their containing construction,
ignoring the separate issue whether constituents which violate this tendency
are significantly less frequent in the middle than at the beginning of the
higher unit.
Writing
before the availability of computers and grammatically-analysed corpora, Yngve
noted (1960: 461) that ‘It is difficult to determine what the actual [depth]
limit is’; his figure of seven seems to have been a surmise based on psychological
findings about memory limitations in other domains, rather than on an empirical
survey of linguistic usage (which would scarcely have been feasible at that
period). Fodor et al. (1974: 414)
echoed Yngve’s point about the difficulty of checking empirically just what the
depth patterns are in real-life usage.
But it is fairly clear that Yngve’s conception involves a sharp
cut-off: up to the depth limit
(whether this is seven or another number) many words are found, beyond the
limit none. He illustrates his
concept with a diagram (reproduced here by permission of the American
Mathematical Society as (1), after Yngve 1961: 134, Fig. 5) of the kind of
structure that would be expected with a depth limit of three; of the fifteen
terminal nodes in (1), apart from the last (which necessarily has depth 0)
there are three at depth 1, six at depth 2, and five at depth 3. Yngve’s caption to the diagram reads
‘If the temporary memory can contain only three symbols, the structures it can
produce are limited to a depth of three and can never penetrate the dotted
line.’
FIG. 1 ABOUT HERE
Yngve’s
depth hypothesis is significant for computational linguistics, because ‹
leaving aside the question whether sentences violating the depth limit should
be regarded as ‘ungrammatical’ or as ‘grammatical but unacceptable’, a
distinction that we shall not discuss ‹ it seems to imply that English
grammatical usage is determined in part by a nonlocal constraint. Since the phrase-structure rules of
English grammar allow some left-branching and are recursive, it appears that
the class of structures they generate should include structures with excessive
left-branching, which would have to be filtered out by a mechanism that
responds to the overall shape of a tree rather than to the relationship between
a mother node and its immediate daughter nodes. Statistical optimizing techniques for automatic parsing,
such as those of Sampson et al. (1989), Black et al. (1993), which select the
analysis for an input string which maximizes a continuous measure of
grammatical plausibility, might need to build depth of left-branching into
their evaluation metrics as a consideration to be traded off against local
mother/daughter-node relationships.
While
there is undoubtedly something right about Yngve’s depth hypothesis, to an
empirically-minded corpus linguist the postulation of a fixed limit to depth of
left-branching has a suspicious air.
Corpus linguists tend rather to think of high- and low-frequency
grammatical configurations, with an ‘impossible’ structure being one that
departs so far from the norm that its probability is in practice
indistinguishable from zero, but without sharp cut-offs between the ‘possible’
and the ‘impossible’. The aim of
this paper is to bring corpus evidence to bear on the task of discovering
precisely what principle lies behind the tendency to asymmetry observed by
Yngve in English. We shall find
that the answer is clear-cut; that it does not imply a sharp cut-off between
acceptable and unacceptable depths of left-branching; and that it has positive
consequences for the computational-tractability issues canvassed above.
2.
Evidence used to assess the hypothesis
The corpus used for this purpose is the SUSANNE
Corpus (Sampson 1995).[2]
This is an approximately 130,000-word subset of the Brown Corpus of
edited American English, equipped with annotations identifying its surface and
logical grammatical structure. The
SUSANNE Corpus was developed in conjunction with the SUSANNE analytic scheme
(op. cit.). This is a set of
annotation symbols and detailed rules for applying them to difficult cases,
which is intended to come as close as possible to the ideal of defining
grammatical analyses for written and spoken English that are predictable (in the sense that different
analysts independently applying the scheme to the same sample of English must
produce identical annotations), comprehensive
(in the sense that everything found in real-life usage receives an analysis,
and all aspects of English surface and logical grammar which are definite
enough to be susceptible of explicit annotation are indicated), and consensual (in that the scheme avoids taking
sides on analytic issues which are contested between rival linguistic theories,
choosing instead a ‘middle-of-the-road’ analysis into which alternative
theorists’ analyses can be translated).
Its 130,000 words make the SUSANNE Corpus far from the largest analysed
corpus of English now available, but limited size is the penalty paid to
achieve high reliability of the analysis of each individual sentence ‹ for
present purposes that is important.[3]
The research reported below used Release 3 of the SUSANNE Corpus,
completed in March 1994; the many
proofreading techniques to which this version was subjected before release
included scanning the entire text formatted by software which uses indentation
to reflect the constituency structure implied by the SUSANNE annotations, so
that most errors which would affect the conclusions of the present research
should have been detected and eliminated.
Although
the SUSANNE analytic scheme aims to be ‘consensual’ as just defined, obviously
many individual linguistic theorists would prefer different structural analyses
for particular constructions.
However, although this might lead to some changes in the individual
figures reported below, the overall conclusions are sufficiently clear-cut to
make it reasonable to hope that they would be unaffected by such modifications,
provided these were carried out consistently.[4]
Some
readers may think it unfortunate that the present investigation is based on
written rather than spoken English; if constraints on left-branching derive
from psychological processing considerations (as Yngve believed) it is likely
that these considerations impact more directly on spontaneous speech than on
writing. At present there is to my
knowledge no analysed corpus of spontaneous spoken English which would have
been suitable for the purpose. But
in any case, transcriptions of spontaneous speech tend not to contain long chains
even of right-branching structure, and they contain many editing phenomena
which make it difficult to analyse an utterance in terms of a single coherent
tree-structure; so that it is questionable whether an analysed corpus of
spontaneous speech could be used for this research, even if we had one. The highly-ramified structures
discussed by Yngve (1960) are in fact much more characteristic of written than
of spoken English, and I believe that an analysed corpus of written English may
offer the best opportunity to take his work further.
3. Preparation of the test data
In order to study
left-branching, it was necessary to modify the structures of the SUSANNE Corpus
in a number of respects:
(i) The SUSANNE analytic scheme treats
punctuation marks as ‘words’ with their own place in parse trees; and it
recognizes ‘ghost’ elements (or ‘empty nodes’) ‹ terminal nodes marking the
logical position of elements which appear elsewhere in surface structure, and
which have no concrete realization of their own. Punctuation marks are not likely to be relevant to our
present concerns (with respect to human syntactic processing they are written
markers of structure rather than elements forming part of a syntactic
structure); and ghost elements are too theory-dependent to be appropriately
included in an empirical investigation such as ours (Yngve discussed only the
structuring of concrete words).
Therefore all terminal nodes of these two types, and any nonterminals
dominating only such nodes, were pruned out of the SUSANNE structures.
(ii) Any tree whose root node is labelled
Oh, ‘heading’, was eliminated:
this covers items such as numbered chapter titles, and other forms whose
internal structure often has little to do with the grammar of running English
text.
(iii) Apart from ‘headings’, the SUSANNE
texts are divided by the analysis into units whose root nodes are labelled O,
‘paragraph’. A paragraph normally
consists of an unstructured chain of sentences (interspersed with
sentence-final punctuation marks which were eliminated at step (i)). Yngve’s thesis relates to structure
within individual sentences; therefore O nodes were eliminated, and the units
within which left-branching was examined were the subtrees whose roots are
daughters of O nodes in the unmodified Corpus. Not all of these units are grammatically ‘complete
sentences’; occasionally, for instance, a noun phrase functions as an immediate
constituent of a SUSANNE paragraph.
The present investigation paid no attention to whether root nodes of
trees in the modified Corpus had the label S or some other label.
(iv) Some SUSANNE tree structures contain
nodes below the root, representing categories such as ‘direct quotation’, which
with respect to their internal constituency are equivalent to root nodes. For the present investigation, the
links between such ‘rootrank nodes’ (Sampson 1995: §4.40) and their daughters
were severed: thus left-branching
was measured within the sentence(s) of a direct quotation without reference to
the sentence within which the quotation was embedded, and when left-branching
was measured in that quoting sentence the quotation was treated as a single
terminal node.
(v) The SUSANNE analytic scheme treats
certain sequences of typographic words, e.g. up to date used as an
adjective, as grammatically equivalent to single words. Any node labelled with an ‘idiomtag’
(Sampson 1995: §3.55) was treated as terminal, and the structure below it in
the unmodified SUSANNE Corpus was ignored.
(vi) The SUSANNE analytic scheme makes
limited use of singulary-branching structure. For instance, a gerundive clause consisting of a present
participle and nothing more will be assigned a node labelled with a clausetag
dominating only a node labelled with a verb-group tag dominating only a node
labelled with a present-participle wordtag. Numerical measures of left-branching might take singulary
branching into account in different ways, depending on exactly how the measures
were defined, but intuitively it seems unlikely that singulary branching is
significant in this connexion; and again singulary-branching nodes seem to be
entities that are too theory-laden to be considered in the present
context. (What would it mean to
assert that the grammatical configuration just cited is a case of three
separate units that happen to be coterminous, rather
than a case of one word unit that happens to play three roles? ‹ many would
see these as different ways of talking about the same facts.) Therefore singulary branching was
eliminated by collapsing pairs of mother and only-daughter nodes into single
nodes.
4. Counts of word depths
The first question put to the resulting set of
sentence structures was whether Yngve’s concept of a sharp limit to the
permissible degree of ‘depth’ is borne out in the data. Let us say that the lineage of a word is the class of nodes
including the leaf node (terminal node) associated with that word, the root
node of its tree, and all the intermediate nodes on the unique path between
leaf and root nodes; and let us say that a node e is a younger sister of a node d if d
and e are immediately dominated by the same ‘mother’ node and e
is further right than d.
Then Yngve’s concept of the ‘depth’ of a word corresponds to:
(2) The
total number of younger sisters of all the nodes in the word’s lineage.
The number of words in the modified SUSANNE Corpus
having various depths in this sense is shown in Table 1.
TABLE 1 ABOUT HERE
Table
1 gives us not a picture of a phenomenon that occurs freely up to a cut-off
point and thereafter not at all, but of one which, above a low depth, becomes
steadily less frequent with increasing depth until, within the finite quantity
of available data, its probability becomes indistinguishable from zero.
However,
although (2) is the definition of ‘depth’ that corresponds most directly to
Yngve’s exposition, there are two aspects of it which might be called into
question. In the first place,
‘depth’ in this sense can arise as much through a single node having many younger
sisters as through a long lineage of nodes each having one younger sister. This is illustrated by the one word in
SUSANNE having depth 13, which is the first word[5] of the sentence Constitutional
government, popular vote, trial by jury, public education, labor unions,
cooperatives, communes, socialized ownership, world courts, and the veto power
in world councils are but a few examples (Brown Corpus and SUSANNE Corpus
location code G11:0310). The
SUSANNE analysis of this sentence is shown in (3); nodes contributing to the
depth count of the first word are underlined.[6]
FIG. 3 ABOUT HERE
Although
in principle the existence of individual nodes with large numbers of daughters
and the existence of long lineages of nodes each having one younger sister are
two quite different aspects of tree-shape, for Yngve the distinction was
unimportant because he believed that branching in English grammatical
structures is always or almost always binary (Yngve 1960: 455). But this seems to have been less an
empirical observation about English grammar than an analytical principle Yngve
chose to impose on English grammar.
In the case of multi-item co-ordinations such as the one in (3), for
instance, where semantics implies no internal grouping of the conjuncts I know
of no empirical reason to assume that the co-ordination should be analysed as a
hierarchy of binary co-ordinations; in SUSANNE analyses, which avoid positing
structure except where there are positive reasons to do so, many nodes have
more than two daughters. Where
SUSANNE has a single node with three or more daughters, it seems that Yngve
regularly assumed a right-branching hierarchy of binary nodes. This implies that ‘depth’ measured on
SUSANNE trees will best approximate to Yngve’s concept if each node having
younger sister(s) contributes exactly one to the depth of the words it
dominates, rather than nodes having many younger sisters making a greater
contribution. In that way, depth
figures for words dominated by nodes with many daughters will be the same as
they would be in the corresponding Yngvean trees containing only binary
nodes. (To make the point quite
explicit: although I do not myself
believe that grammatical branching is always binary, I am proposing that we
count word depth in a way that gives the same results whether that is so or not.)
Secondly,
even the most right-branching tree must have an irreducible minimum of left
branches. A tree in which all
nonterminal nodes other than the root are rightmost daughters ought surely to
be described as containing no left-branching at all; yet by Yngve’s definition
each word other than the last will have a depth of one, rather than zero (and
the average word depth will consequently depend on how many words there
are). This inconsistency could be
cured by ignoring the leaf node when counting left-branching in a lineage.
Accordingly,
I suggest that a more appropriate definition than (2) of the depth of a word
would be:
(4) The
total number of those nonterminal nodes in the word’s lineage which have at
least one younger sister.
Thus, consider terminal node e in tree (5):
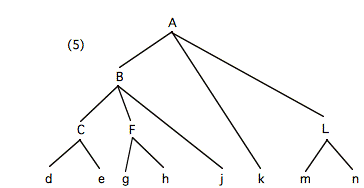
Counted according to (2), the depth of e is
four, the relevant younger sister nodes being F, j, k, L. Counted according to (4), the depth of e
is two, the contributing nonterminals being B and C. If the distribution of depths among
SUSANNE words is recomputed using definition (4), the results are given in
Table 2.
TABLE 2 ABOUT HERE
The
decline is now much steeper, but again we seem to be looking at a continuously
decreasing probability which eventually becomes indistinguishable from zero in
a finite data-set, rather than at a sharp cut-off. The four words at depth 5 are the words New York, United
States occurring in the respective sentences Two errors by New York
Yankee shortstop Tony Kubek in the eleventh inning donated four unearned runs
and a 5-to-2 victory to the Chicago White Sox today (A11:1840), and Vital
secrets of Britain’s first atomic submarine, the Dreadnought, and, by
implication, of the entire United States navy’s still-building nuclear sub
fleet, were stolen by a London-based soviet spy ring, secret service agents
testified today (A20:0010).
These examples seem intuitively to relate more closely than the (3)
example to the depth phenomenon with which Yngve was concerned; their SUSANNE
analyses are (6) and (7).
FIG.
6 ABOUT HERE
FIG.
7 ABOUT HERE
It
is true that, if depth is counted in terms of definition (4) rather than
Yngve’s original definition (2), then Table 2 shows that the SUSANNE data are
logically compatible with a fixed maximum depth of seven. But to explain the figures of Table 2
in terms of a fixed depth limit is scientifically unsatisfactory, because it is
too weak a hypothesis to account for the patterning in the data. To give an analogy: a table of the numbers of
twentieth-century Europeans who attain various ages at death would, in the
upper age ranges, show declining figures for increasing age until zero was
reached at some age in the vicinity of 120. Logically this would be compatible with a theory that human
life is controlled by a biological clock which brings about death at age 125
unless the person happens to die earlier; but such a theory would be
unconvincing. In itself it fails
to explain why we do not meet numerous 124-year-olds ‹ to explain that we need
some theory such as cumulative genetic transcription errors as cells repeatedly
divide leading to increased probability of fatal maladies; and, if we adopt a
theory of this latter kind, it is redundant also to posit a specific fixed
maximum which is rarely or never attained.
What
we would like to do is to find some numerical property obeyed by the SUSANNE
trees which is more specific than ‘no depth greater than seven’, which is
invariant as between short and long sentences, and which predicts that the
number of words at a given depth will decline as depth increases.
In
the following sections I address this issue in the abstract, prescinding from
psychological questions about how human beings might produce or understand
grammatical structures, and instead treating the set of observed SUSANNE
parsetrees purely as a collection of shapes in which some invariant property is
sought. The ratio of psychological
theorizing to empirical description in this area has been rather high to date,
and the balance deserves to be redressed.
Having found an empirical result I shall not wholly refrain from
speculation about possible processing implications, but these will be very
tentative; the central aim of the work reported here is to establish the
empirical facts rather than to draw psychological conclusions.
5. Alternative measures of
left-branching
One possible invariant might be mean depth (in the
(4) sense) of the various words in a sentence. If there were no tendency to avoid left-branching, then mean
word depth would be higher in long sentences than in short sentences, because
more words imply longer lineages between terminal nodes and root, and the
lineages would contain left-branching as frequently as right-branching. Yngve’s picture of a depth boundary
that remains fixed however long a sentence grows suggests that mean word depth
might be constant over different sentence lengths; this could be true despite
the occasional incidence of words with unusually large depth figures.
However,
if we choose to compute the asymmetry of sentence structures by an averaging
procedure over all parts of the tree, rather than by taking a single maximum
figure, then averaging word depth is not the only way to do this. Two other possibilities present themselves. One could take the mean, over the nonterminal
nodes, of the proportion of each node’s daughters which are left-branching
nodes ‹ that is, which are
themselves nonterminal and are not the rightmost daughter. Or one could take the mean, again over
the nonterminal nodes, of the proportion of all words ultimately dominated by a
node which are not dominated by the rightmost daughter of the node and are not
immediately dominated by the node.
Let us call these three statistical properties of a tree structure the depth-based measure, the production-based measure, and the realization-based
measure respectively.
A
low figure for any of these three measures implies that a tree has relatively
little left-branching. But the
measures are not equivalent.
Consider for instance the three six-leaf tree structures (8), (9), and
(10):
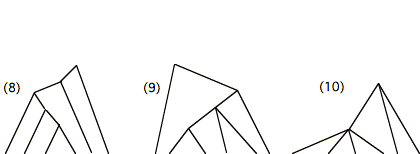
By the depth-based measure, the most left-branching
of the three structures is (8); by the production-based measure, the most
left-branching is (9); by the realization-based measure, the most
left-branching is (10).[7]
So far as I am aware, other methods of calculating degree of
left-branching will assign a ranking to the various trees having a given number
of leaf nodes that will be identical or near-identical to the ranking assigned
by one of these three measures.
None
of the three measures give figures for different trees which are directly
comparable when the trees have different numbers of leaf nodes (i.e. dominate
sentences of different lengths).
An entirely right-branching tree, in which nonterminal nodes are always
rightmost daughters of their mothers, will score zero by each of the three
measures. But, for each of the
measures, the score for an entirely left-branching tree will depend on sentence
length. Writing w for the
number of leaf nodes (words) dominated by a tree, the maximum score will be:
for
the depth-based measure
for
the production-based measure
for
the realization-based measure
[Consult print publication for formulae missing in this online version]
We might therefore normalize the measures to a common
scale by dividing the raw figures by the appropriate one of these three
quantities. The resulting
normalized measures give us a meaningful way of comparing the positions
occupied by sentences of any lengths on a scale from 1, for ‘completely
left-branching’, to 0, for ‘completely right-branching’ (with respect to any
one of the three definitions of asymmetry).
I
shall refer to the six resulting statistical measures of left-branching as RD,
RP, RR, ND, NP, NR, for raw v. normalized depth-, production-, and realization-based
measures. The question now is
which, if any, of these six measures yields figures for structural asymmetry in
English that show little variance with different lengths of sentence.
6. Incidence of left-branching computed by
alternative measures
In order to answer this question I grouped the
sentences of the modified SUSANNE Corpus into sets by length; for each set up
to length w = 47 I computed the six asymmetry measures for the sentences
in the set, and took their means.
(The maximum length of sentences examined was fixed at 47 because, above
this length, not all lengths are represented in the data by at least ten
instances. Up to w = 47 the
fewest instances of a sentence-length is nineteen for w = 45.) For very short sentences the means
display some patternless fluctuations, which is not too surprising: with few words and even fewer
nonterminals to average over, one should perhaps not expect statistical
measures of a tree’s topological properties to be very informative.[8]
But the runs of figures from w = 7 up to w = 47
(covering a total of 5963 sentences) display very clear trends, summarized in
Table 3, which for each of the six measures gives the overall mean and standard
deviation of the 41 individual means for different sentence lengths, together
with the linear correlation coefficient r between sentence length and
individual mean asymmetry figure.
TABLE 3 ABOUT HERE
The
measure closest to Yngve’s concept, RD, shows a very strong positive
correlation (r = 0.96) between length and depth: individual mean RD figures range from
0.38 for 8-word sentences up to 0.98 for 47-word sentences. Normalizing the depth measure merely
reverses the sign of the correlation (r = –0.93): individual mean ND figures range
between 0.136 for length 7 and 0.040 for length 41.
By
far the most consistent measure of left-branching is RP, which shows
essentially no correlation with sentence length (r = 0.093). Mean RP figures for different sentence
lengths cluster tightly (low standard deviation) round the overall mean of
0.094; the lowest individual mean is 0.084 for length 45, the highest is 0.102
for length 44. It is evidently RP
which gives rise to the limited left-branching which Yngve took for an absolute
bar on lineages containing more than a fixed maximum number of left branches.
The
normalized production-based measure of left-branching, and the
realization-based measures, are not as precisely correlated with sentence
length as the depth-based measures, but absolute correlation coefficients over
0.6 make it clear that these measures are not candidates for the invariant
quantity adumbrated by Yngve.
Individual means range from 0.22 (NP), 0.123 (RR), 0.189 (NR), for
length 7, down to 0.17 (NP), 0.085 (RR), 0.094 (NR), for length 45.
I
do not suggest that the incidence of words at different Yngvean depths can be
predicted purely from statistics on the average incidence of nonterminal and
terminal daughters in individual productions. If that were possible, the figures of Table 2 would display
a regularity that we do not find.
Assuming that not only the proportion L of left-branching
daughters but also the mean number b of daughter nodes per mother node,
and the proportion R of rightmost daughters which are nonterminal, are
constant for different sentence-lengths, then each figure in Table 2 ought to
differ by a constant factor bL/(1 – R) from its
predecessor. Even if the figures
of Table 2 were not to hand, we would know that things are not that simple. The great majority of root nodes in the
modified SUSANNE Corpus have the same label S, ‘main clause’, and the class of
those productions which share some particular mother label will not in general
contain the same proportion of left-branching daughters as found in all
productions (the fact, recorded in Table 2, that there are more depth-1 than
depth-0 words in the Corpus shows that productions having S to the left of the
arrow have a relatively high proportion of left-branching daughters). Likewise the mean proportion of
left-branching daughters for category labels which themselves occur on
left-branching daughter nodes is very likely to deviate from the overall mean
in one direction or the other.
Considerations like these imply that we cannot predict an expected
pattern of word depths against which Table 2 can be tested. But, once we know that the overall
incidence of left-branching productions is a low constant frequency for
sentences of different lengths, there is no need of further explanation for the
fact that the figures in Table 2 dwindle to zero after the first few rows, and
hence for Yngve’s impression that depths above about seven never occur in
practice.[9]
7. Implications of the findings
From a computational perspective, the significance of
the fact that RP is the invariant measure is that this is the one measure of
asymmetry which depends purely on local grammatical facts. A context-free grammar with
probabilities associated with alternative productions gives an invariant mean
RP figure for sentences of different lengths; if any of the other five measures
had proved to be invariant with sentence length, that would have implied some
mechanism controlling global tree shape, separate from the class of allowable
productions. Thus the finding may
represent good news for computational tractability.
Admittedly,
even the invariance of RP might require an explanation in nonlocal terms, if
the grammatical structures to be explained were to incorporate the singulary
branching which was eliminated from the modified SUSANNE Corpus (§3, (vi)
above). For instance, if pronouns
are introduced into clauses via rules which rewrite clause categories as
sequences including the category ‘noun phrase’ at different points, and
separate rules which rewrite ‘noun phrase’ alternatively as a pronoun or a
multi-word sequence, then a probabilistic context-free grammar could not ensure
that subjects are commonly pronouns and that multi-word noun phrases occur much
more often clause-finally. But the
grammar of English could be defined without singulary branching, by using rules
in which e.g. pronouns occur directly in the expansions of clause categories.
It
is interesting that the invariant measure is RP rather than NP. One interpretation of this finding
might perhaps be that sentences are not in practice constructed by choosing the
words they are to contain and then organizing those words into a suitable
grammatical structure; rather, the grammatical structures are chosen
independently of sentence-length considerations, and the expansion process
terminates simply because productions having no nonterminals to the right of
the arrow have a certain probability and hence will sooner or later be chosen.[10]
It
is hard to accept that the consistent mean left-branching figure for English
productions could be caused by a fixed limit to the number of items held in the
speaker’s/writer’s short-term memory, as Yngve argued: that mechanism would give invariant RD
rather than invariant RP figures.
If the language used low frequency of left-branching productions (that
is, productions which add one to the Yngvean depth of the words ultimately
dominated by their left-branching daughter node) as a strategy to avoid
generating trees containing words deeper than some fixed limit such as seven,
it would be a very inefficient strategy:
most words would be at a depth much less than the limit, ‘wasting’
available memory, and even so there would occasionally be a violation of the
limit. I suggest that fixed
numerical limits may play little role in the psychological processing of
language.
It
would be interesting to discover whether the different incidence of Yngvean
depth found in languages such as Japanese and Turkish can equally be accounted
for by left-branching production frequencies fixed at different
language-specific values.
8. Summary
We have seen that Yngve was right in saying that
English grammatical usage embodies a systematic bias against left-branching
constructions. But corpus evidence
of a kind that has become available only since Yngve published his hypothesis
suggests that the nature of that bias is rather different from what Yngve seems
to have supposed. It is not that
English enforces a left-branching depth maximum which is frequently reached but
never exceeded. Rather, there is a
specific probability of including a left-branching nonterminal category among
the immediate constituents of a construction; this probability is independent
of the wider sentence structure within which the construction is embedded, but
because the probability is small the incidence of words at different depths
becomes lower, and eventually vanishingly low, at greater depths.
REFERENCES
Aho, A. V., Hopcroft, J. E., & Ullman,
J. D. (1974). The design and
analysis of computer algorithms.
Reading, Mass.:
Addison-Wesley.
Black, E., Garside, R. G., & Leech, G.
N. (eds.) (1993). Statistically-driven
computer grammars of English: the IBM/Lancaster approach. Language and Computers: Studies in
Practical Linguistics 8.
Amsterdam: Rodopi.
Booth, T. L. & Thompson, R. A.
(1973). Applying probability
measures to abstract languages. IEEE
Transactions on Computers C-22.
442-450.
Church, K. W. (1982). On memory limitations in natural
language processing.
Bloomington, Indiana:
Indiana University Linguistics Club.
De Roeck, Anne, Johnson, R., King,
Margaret, Rosner, M., Sampson, G. R., & Varile, N. (1982). A myth about centre-embedding. Lingua 58. 327-340.
Ellegård, A. (1978). The syntactic structure of English
texts: a computer-based study of four kinds of text in the Brown University
Corpus. Gothenburg Studies in
English 43. Gothenburg: Acta Universitatis Gothoburgensis.
Fodor, J. A., Bever, T. G., & Garrett,
M. F. (eds.) (1974). The psychology of language: an introduction
to psycholinguistics and generative grammar. London:
McGraw-Hill.
Hofland, K. & Johansson, S.
(1982). Word frequencies in
British and American English.
Bergen: Norwegian Computing Centre for the Humanities.
Householder, F.W. (ed.) (1972). Syntactic theory 1: structuralist. Harmondsworth, Mddx: Penguin.
Jakobson, R. (ed.) (1961). Structure of language and its
mathematical aspects.
Proceedings of Symposia in Applied Mathematics 12. Providence, Rhode Island: American Mathematical Society.
Knuth, D. E. (1973). The art of computer programming:
vol. 3, sorting and searching.
Reading, Mass.:
Addison-Wesley.
Lees, R. B. (1961). Comments on Hockett’s paper. In Jakobson, ed. (1961). 266-267.
Lyons, J. (1991). Chomsky. (3rd edition.) London: Fontana.
Miller, G. A. & Chomsky, A. N.
(1963). Finitary models of
language users. In Luce, R. D.,
Bush, R. R., & Galanter, E. (eds.), Handbook of mathematical psychology,
vol. 2. London: Wiley.
Reich, P. A. (1969). The finiteness of natural
language. Language 45. 831-843. (Reprinted in Householder, ed. (1972). 258-272.)
Sampson, G. R. (1995). English
for the computer: the
SUSANNE Corpus and analytic scheme.
Oxford: Clarendon Press.
Sampson, G. R. (1996). From
central embedding to corpus
linguistics.
Sampson, G. R., Haigh, R., & Atwell,
E. S. (1989). Natural language
analysis by stochastic optimization: a progress report on Project APRIL. Journal of Experimental and
Theoretical Artificial Intelligence 1. 271-287.
Stabler, E. P., Jr (1991). Avoid the pedestrian’s paradox. In Berwick, R. C., Abney, S. P., &
Tenny, Carol (eds.) Principle-based parsing: computation and
psycholinguistics.
London: Kluwer. 199-237.
Stabler, E.P. (1994). The finite connectivity of linguistic
structure. In Clifton, C., Jr,
Frazier, Lyn, & Rayner, K. (eds.) Perspectives on sentence processing. Hillsdale, N.J.: Lawrence Erlbaum. 303-336.
Steedman, M. J. (1989). Grammar, interpretation, and processing
from the lexicon. In
Marslen-Wilson, W. (ed.) Lexical representation and process. London: MIT Press.
463-504.
Tesnière, L. (1965). Eléments de syntaxe structurale
(2nd ed.). Paris: Klincksieck.
Yngve, V. H. (1960). A model and an hypothesis for language
structure. Proceedings of the
American Philosophical Society 104.
444-466.
Yngve, V. H. (1961). The depth hypothesis. In Jakobson, ed. (1961). 130-138. (Reprinted in Householder, ed. (1972). 115-123.)
Depth Words
0 7851
1 30798
2 34352
3 26459
4 16753
5 9463
6 4803
7 2125
8 863
9 313
10 119
11 32
12 4
13 1
14+ 0
Table
1
Depth counts by Yngve’s definition
Depth Words
0 55866
1 64552
2 12164
3 1274
4 76
5 4
6+ 0
Table
2
Depth counts by revised definition
RD ND RP NP RR NR
mean 0.73 0.067 0.094 0.20 0.10 0.12
s.d. 0.19 0.023 0.0038 0.0091 0.0075 0.020
r 0.96 –0.93 0.093 –0.61 –0.83 –0.88
Table
3
Distribution
of mean structural asymmetry at different sentence lengths, for six measures of
asymmetry
Raw Depth-Based Measure (RD): word depth (by definition (3)),
averaged over the words of a sentence
Raw Production-Based Measure (RP): proportion of the daughters of a
nonterminal node which are themselves nonterminal and nonrightmost, averaged
over the nonterminals of a sentence
Raw Realization-Based Measure (RR): proportion of the words dominated by a
nonterminal which are also dominated by a lower nonterminal that is not the
rightmost daughter, averaged over the nonterminals of a sentence
Normalized Measures (ND, NP, NR): for each sentence the corresponding raw
measure is converted to a number between 0 and 1 by dividing by the largest
possible raw figure for a sentence of the same length
Address:
School of Cognitive and Computing Sciences
University of Sussex
Falmer, Brighton BN1 9QH